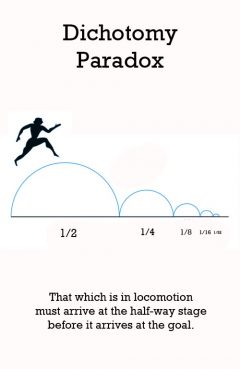
Release Message:  That which is in locomotion must arrive at the half-way stage before it arrives at the goal. Authored by Zeno.

Description:  That which is in locomotion must arrive at the half-way stage before it arrives at the goal._ as recounted by Aristotle, Physics VI:9, 239b10 ii. The Dichotomy (The Racetrack) In his Progressive Dichotomy Paradox, Zeno argued that a runner will never reach the stationary goal line of a racetrack. The reason is that the runner must first reach half the distance to the goal, but when there he must still cross half the remaining distance to the goal, but having done that the runner must cover half of the new remainder, and so on. If the goal is one meter away, the runner must cover a distance of 1/2 meter, then 1/4 meter, then 1/8 meter, and so on ad infinitum. The runner cannot reach the final goal, says Zeno. Why not? There are few traces of Zeno's reasoning here, but for reconstructions that give the strongest reasoning, we may say that the runner will not reach the final goal because there is too far to run, the sum is actually infinite. The Standard Solution argues instead that the sum of this infinite geometric series is one, not infinity. Suppose Homer wishes to walk to the end of a path. Before he can get there, he must get halfway there. Before he can get halfway there, he must get a quarter of the way there. Before traveling a quarter, he must travel one-eighth; before an eighth, one-sixteenth; and so on. This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility. The dichotomy This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion. An alternative conclusion, proposed by Henri Bergson, is that motion (time and distance) is not actually divisible. This argument is called the Dichotomy because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.[11] There are two versions of the dichotomy paradox. In the other version, before Homer could reach the end of the path, he must reach half of the distance to it. Before reaching the last half, he must complete the next quarter of the distance. Reaching the next quarter, he must then cover the next eighth of the distance, then the next sixteenth, and so on. There are thus an infinite number of steps that must first be accomplished before he could reach the end of the path. Expressed this way, the dichotomy paradox is very much analogous to that of Achilles and the tortoise.