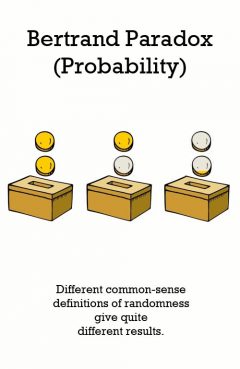
Release Message:  After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold is 1 2; in fact, the probability is actually 2 3. Authored by Joseph Bertrand.

Description:  The Bertrand paradox is a problem within the classical interpretation of probability theory. Joseph Bertrand introduced it in his work Calcul des probabilit s (1889) as an example to show that probabilities may not be well defined if the mechanism or method that produces the random variable is not clearly defined. Bertrand's box paradox is a classic paradox of elementary probability theory. It was first posed by Joseph Bertrand in his Calcul des probabilit_s, published in 1889. There are three boxes: a box containing two gold coins, a box with two silver coins, and a box with one of each. After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold is 1 2; in fact, the probability is actually 2 3. Two problems that are very similar are the Monty Hall problem and the Three Prisoners problem. These simple but slightly counterintuitive puzzles are used as a standard example in teaching probability theory. Their solution illustrates some basic principles, including the Kolmogorov axioms. --------------- The paradox as stated by Bertrand[edit source | editbeta] It can be easier to understand the correct answer if you consider the paradox as Bertrand originally described it. After a box has been chosen, but before a drawer is opened to let you observe a coin, the probability is 2/3 that the box has two of the same kind of coin. If the probability of "observing a gold coin" in combination with "the box has two of the same kind of coin" is 1/2, then the probability of "observing a silver coin" in combination with "the box has two of the same kind of coin" must also be 1/2. And if the probability that the box has two like coins changes to 1/2 no matter what kind of coin is shown, the probability would have to be 1/2 even if you hadn't observed a coin this way. Since we know his probability is 2/3, not 1/2, we have an apparent paradox. It can be resolved only by recognizing how the combination of "observing a gold coin" with each possible box can only affect the probability that the box was GS or SS, but not GG.