Barbershop Paradox
Release Date: 7//1894
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The supposition that if one of two simultaneous assumptions leads to a contradiction, the other assumption is also disproved leads to paradoxical consequences. Authored by Lewis Carroll.
Description: The Barbershop paradox was proposed by Lewis Carroll in a three-page essay titled "A Logical Paradox", which appeared in the July 1894 issue of Mind. The name comes from the "ornamental" short story that Carroll uses to illustrate the paradox (although it had appeared several times in more abstract terms in his writing and correspondence before the story was published). Carroll claimed that it illustrated "a very real difficulty in the Theory of Hypotheticals" in use at the time.[1]" What the Tortoise Said to Achilles" //// Barbershop Paradox
Beauty Contest Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: People's selections are based not on an item's fundamental value, but rather on what they think everyone else thinks their value is.
Description: People's selections are based not on an item's fundamental value, but rather on what they think everyone else thinks their value is.
Bell's Spaceship Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Concerning relativity.
Description: Bell's spaceship paradox is a thought experiment in special relativity. It was first designed by E. Dewan and M. Beran in 1959 and became more widely known when J. S. Bell included a modified version. In the inertial frame S, a delicate string or thread hangs between two identically accelerating spaceships. Both rockets and the thread all move at all times with the same velocity in S and are therefore all subject to the same Lorentz contraction, so the entire assembly seems to be contracted in the S frame the same way. Therefore at first sight it might appear that the thread will not break during acceleration. This argument, however, is incorrect as shown by Dewan & Beran and Bell. The distance between the spaceships does not undergo Lorentz contraction with respect to the distance at the start, because in S it is effectively defined to remain the same, due to the same acceleration of both spaceships. It also turns out that the proper length between the two has increased in the frames in which they are momentarily at rest (S'), because the accelerations of the spaceships are unequal here. The thread, on the other hand, being a physical object held together by electrostatic forces, maintains the same proper length. Thus in frame S it must be Lorentz contracted, which result can also be derived when the electromagnetic fields of bodies in motion are considered. So the thread must break in both frames: In S' due to the unequal acceleration and the increasing distance between the spaceships, in S due to length contraction of the thread. In general, it was concluded by Dewan & Beran and Bell, that relativistic stresses arise when all parts of an object are accelerated the same way with respect to an inertial frame, and that length contraction has real physical consequences. However, while agreeing with the result that the thread will break and that relativistic stresses will occur, some authors disagree with the interpretation that this proves the "physical reality" of length contraction. They argue that relativistic acceleration is the sole cause for the breaking of the thread in all frames of reference, not length contraction. J. S. Bell (John Stewart Bell)
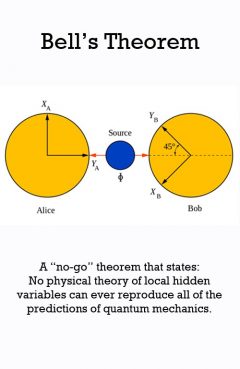
Bell's Theorem
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Why do measured quantum particles not satisfy mathematical probability theory? Authored by J. S. Bell.
Description: Bell's Theorem Bell's theorem is a no-go theorem famous for drawing an important line in the sand between quantum mechanics (QM) and the world as we know it classically. In its simplest form, Bell's theorem states: No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics. When introduced in 1927, the philosophical implications of the new quantum theory were troubling to many prominent physicists of the day, including Albert Einstein. In a well known 1935 paper, Einstein and co-authors Boris Podolsky and Nathan Rosen (collectively EPR) demonstrated by a paradox that QM was incomplete. This provided hope that a more complete (and less troubling) theory might one day be discovered. But that conclusion rested on the seemingly reasonable assumptions of locality and realism (together called "local realism" or "local hidden variables", often interchangeably). In the vernacular of Einstein: locality meant no instantaneous ("spooky") action at a distance; realism meant the moon is there even when not being observed. These assumptions were hotly debated within the physics community, notably between Nobel laureates Einstein and Niels Bohr. In his groundbreaking 1964 paper, "On the Einstein Podolsky Rosen paradox", physicist John Stewart Bell presented an analogy (based on spin measurements on pairs of entangled electrons) to EPR's hypothetical paradox. Using their reasoning, he said, a choice of measurement setting here should not affect the outcome of a measurement there (and vice versa). After providing a mathematical formulation of locality and realism based on this, he showed specific cases where this would be inconsistent with the predictions of QM. J. S. Bell (John Stewart Bell)
Benardette's Paradox (Paradox of the Gods)
Release Date: //1964
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: How far can a man walk if an infinity of gods intends to stop him? Authored by J. A. Bernadete.
Description: A man walks a mile from a point. But there is an infinity of gods each of whom, unknown to the others, intends to obstruct him. One of them will raise a barrier to stop his further advance if he reaches the half-mile point, a second if he reaches the quarter-mile point, a third if he goes one-eighth of a mile, and so on ad infinitum. So he cannot even get started, because however short a distance he travels he will already have been stopped by a barrier. But in that case no barrier will rise, so that there is nothing to stop him setting off. He has been forced to stay where he is by the mere unfulfilled intentions of the gods. M. Clark, Paradoxes from A to Z
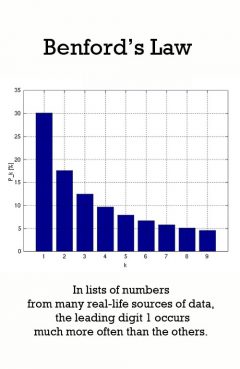
Benford's Law
Release Date: //1938
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In lists of numbers from many real-life sources of data, the leading digit 1 occurs much more often than the others. Authored by Frank Albert Benford, Jr.
Description: Benford's Law, also called the First-Digit Law, refers to the frequency distribution of digits in many (but not all) real-life sources of data. In this distribution, 1 occurs as the leading digit about 30% of the time, while larger digits occur in that position less frequently: 9 as the first digit less than 5% of the time. Benford's Law also concerns the expected distribution for digits beyond the first, which approach a uniform distribution. This result has been found to apply to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical and mathematical constants, and processes described by power laws (which are very common in nature). It tends to be most accurate when values are distributed across multiple orders of magnitude. The graph here shows Benford's Law for base 10. There is a generalization of the law to numbers expressed in other bases (for example, base 16), and also a generalization from leading 1 digit to leading n digits. It is named after physicist Frank Benford, who stated it in 1938,[1] although it had been previously stated by Simon Newcomb in 1881.
Bentley's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In a Newtonian universe, gravitation should pull all matter into a single point. Authored by Richard Bentley.
Description: Bentley's paradox is a cosmological paradox pointing to a problem occurring when Newton's theory of the gravitation is applied to cosmology: "According to Newton, each star in the universe ought to be attracted towards every other star. They should not remain motionless, at a constant distance from each other, but should all fall together to some central point. Newton admitted as much in a letter to Richard Bentley, a leading Cambridge philosopher of the time. The solution for this paradox is that, all the stars are not influenced by one gravitational force but there are many forces acting on the body, hence, forcing it to be either temporarily stationary, or to undergo very slight motion. The theory of Big Crunch suggests a similar thing, that the Universe will collapse by a bang at a point where all matter meets."
Berkson's Paradox (aka Berkson's Bias and Berkson's Fallacy)
Release Date: 6//1946
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Two independent events become conditionally dependent (negatively dependent) given that at least one of them occurs. Authored by Joseph Berkson.
Description: Berkson's paradox or Berkson's fallacy is a result in conditional probability and statistics which is counterintuitive for some people, and hence a veridical paradox. It is a complicating factor arising in statistical tests of proportions. Specifically, it arises when there is an ascertainment bias inherent in a study design. It is often described in the fields of medical statistics or biostatistics, as in the original description of the problem by Joseph Berkson.
The Berry Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The phrase "the first number not nameable in under ten words" appears to name it in nine words. Authored by G. G. Berry.
Description: Consider the expression: "The smallest positive integer not definable in under eleven words." Since there are finitely many words, there are finitely many phrases of under eleven words, and hence finitely many positive integers that are defined by phrases of under eleven words. Since there are infinitely many positive integers, this means that there are positive integers that cannot be defined by phrases of under eleven words. If there are positive integers that satisfy a given property, then there is a smallest positive integer that satisfies that property; therefore, there is a smallest positive integer satisfying the property "not definable in under eleven words". This is the integer to which the above expression refers. The above expression is only ten words long, so this integer is defined by an expression that is under eleven words long; it is definable in under eleven words, and is not the smallest positive integer not definable in under eleven words, and is not defined by this expression. This is a paradox: there must be an integer defined by this expression, but since the expression is self-contradictory (any integer it defines is definable in under eleven words), there cannot be any integer defined by it.
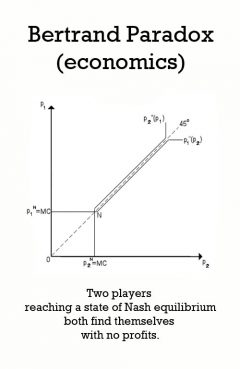
Bertrand Paradox (economics)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Two players reaching a state of Nash equilibrium both find themselves with no profits. Authored by Joseph Bertrand.
Description: In economics and commerce, the Bertrand paradoxnamed after its creator, Joseph Bertrand describes a situation in which two players (firms) reach a state of Nash equilibrium where both firms charge a price equal to marginal cost. The paradox is that in models such as Cournot competition, an increase in the number of firms is associated with a convergence of prices to marginal costs. In these alternative models of oligopoly a small number of firms earn positive profits by charging prices above cost. Suppose two firms, A and B, sell a homogeneous commodity, each with the same cost of production and distribution, so that customers choose the product solely on the basis of price. It follows that demand is infinitely price-elastic. Neither A nor B will set a higher price than the other because doing so would yield the entire market to their rival. If they set the same price, the companies will share both the market and profits. On the other hand, if either firm were to lower its price, even a little, it would gain the whole market and substantially larger profits. Since both A and B know this, they will each try to undercut their competitor until the product is selling at zero economic profit. This is the pure-strategy Nash equilibrium. Recent work has shown that there may be an additional mixed-strategy Nash equilibrium with positive economic profits. The Bertrand paradox rarely appears in practice because real products are almost always differentiated in some way other than price (brand name, if nothing else); firms have limitations on their capacity to manufacture and distribute; and two firms rarely have identical costs. Bertrand's result is paradoxical because if the number of firms goes from one to two, the price decreases from the monopoly price to the competitive price and stays at the same level as the number of firms increases further. This is not very realistic, as in reality, markets featuring a small number of firms with market power typically charge a price in excess of marginal cost. The empirical analysis shows that in most industries with two competitors, positive profits are made. Solutions to the Paradox attempt to derive solutions that are more in line with solutions from the Cournot model of competition, where two firms in a market earn positive profits that lie somewhere between the perfectly competitive and monopoly levels.
Bertrand Paradox (probability)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold is 1 2; in fact, the probability is actually 2 3. Authored by Joseph Bertrand.
Description: The Bertrand paradox is a problem within the classical interpretation of probability theory. Joseph Bertrand introduced it in his work Calcul des probabilit s (1889) as an example to show that probabilities may not be well defined if the mechanism or method that produces the random variable is not clearly defined. Bertrand's box paradox is a classic paradox of elementary probability theory. It was first posed by Joseph Bertrand in his Calcul des probabilit_s, published in 1889. There are three boxes: a box containing two gold coins, a box with two silver coins, and a box with one of each. After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold is 1 2; in fact, the probability is actually 2 3. Two problems that are very similar are the Monty Hall problem and the Three Prisoners problem. These simple but slightly counterintuitive puzzles are used as a standard example in teaching probability theory. Their solution illustrates some basic principles, including the Kolmogorov axioms. --------------- The paradox as stated by Bertrand[edit source | editbeta] It can be easier to understand the correct answer if you consider the paradox as Bertrand originally described it. After a box has been chosen, but before a drawer is opened to let you observe a coin, the probability is 2/3 that the box has two of the same kind of coin. If the probability of "observing a gold coin" in combination with "the box has two of the same kind of coin" is 1/2, then the probability of "observing a silver coin" in combination with "the box has two of the same kind of coin" must also be 1/2. And if the probability that the box has two like coins changes to 1/2 no matter what kind of coin is shown, the probability would have to be 1/2 even if you hadn't observed a coin this way. Since we know his probability is 2/3, not 1/2, we have an apparent paradox. It can be resolved only by recognizing how the combination of "observing a gold coin" with each possible box can only affect the probability that the box was GS or SS, but not GG.
Birthday Paradox (aka The Birthday problem)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In a set of randomly chosen people, some pair of them will have the same birthday.
Description: In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are 366 possible birthdays, including February 29). However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people. These conclusions include the assumption that each day of the year (except February 29) is equally probable for a birthday. The history of the problem is obscure. W. W. Rouse Ball indicated (without citation) that it was first discussed by Harold Davenport. However, Richard von Mises proposed an earlier version of what we consider today to be the birthday problem. The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of cracking a hash function. Mathematical / Logical
Black Hole Information Paradox
Blub Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Cognitive lock of some experienced programmers that prevents them from properly evaluating the quality of programming languages which they do not know.
Description: Cognitive lock of some experienced programmers that prevents them from properly evaluating the quality of programming languages which they do not know.
Bonini's Paradox
Release Date: //1963
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: As a model of a complex system becomes more complete, it becomes less understandable. Authored by Charles Bonini.
Description: Bonini's Paradox named after Stanford business professor Charles Bonini, explains the difficulty in constructing models or simulations that fully capture the workings of complex systems (such as the human brain).[1] In modern discourse, the paradox was articulated by John M. Dutton and William H. Starbuck[2] "As a model of a complex system becomes more complete, it becomes less understandable. Alternatively, as a model grows more realistic, it also becomes just as difficult to understand as the real-world processes it represents" (Computer Simulation of Human Behaviour, 1971). This paradox may be used by researchers to explain why complete models of the human brain and thinking processes have not been created and will undoubtedly remain difficult for years to come. This same paradox was observed earlier from a quote by Paul Val ry, "Everything simple is false. Everything which is complex is unusable." (Notre destin et les lettres, 1937) Also, the same topic has been discussed by Richard Levins in his classic essay "The Strategy of Model Building in Population Biology", in stating that complex models have 'too many parameters to measure, leading to analytically insoluble equations that would exceed the capacity of our computers, but the results would have no meaning for us even if they could be solved. (See Orzack and Sober, 1993; Odenbaugh, 2006). The problem that emerges when the model of a phenomenon is just as hard to explain as the phenomenon it is supposed to explain. The less information a model carries about its subject, the less useful it's going to be in helping someone understand that subject. And yet, the more information a model carries about its subject, the less useful it's going to be in helping someone understand any single point of that subject.
Bootstrap Paradox (also known as Ontological paradox)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Can a time traveler send himself information with no outside source?
Description: The Bootstrap Paradox is a theoretical paradox of time travel that occurs when an object or piece of information sent back in time becomes trapped within an infinite cause-effect loop in which the item no longer has a discernible point of origin, and is said to be ñuncausedî or ñself-createdî. The term "bootstrap paradox" refers to the expression "pulling yourself up by your bootstraps"; the use of the term for the time-travel paradox was popularized by Robert A. Heinlein's story By His Bootstraps.
Borel-Kolmogorov Paradox (Borel's Paradox)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Conditional probability density functions are not invariant under coordinate transformations. Authored by Emile Borel and Andrey Kolmogorov.
Description: In probability theory, the Borel-Kolmogorov paradox (sometimes known as Borel's paradox) is a paradox relating to conditional probability with respect to an event of probability zero (also known as a null set). The fact that the conditional probability distribution over the prime meridian is different from the conditional probability distribution over the equator is puzzling because because a prime meridian in one coordinate system is an equator in another coordinate system,
Bottle Imp Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message:
Description: The premise of the story creates a logical paradox similar to the unexpected hanging paradox. Clearly no rational person would buy it for one cent as this would make it impossible for it to be sold at a loss. However, it follows that no rational person would buy it for two cents either if it is later to be sold only to a rational person for a loss. By induction, the bottle cannot be sold for any price in a perfectly rational world. And yet, the actions of the people in the story do not seem particularly unwise. The story shows that the paradox could be resolved by the existence of certain characters: ´ Someone who loves the bottle's current owner enough to sacrifice his or her own soul for that person. ´ Someone who believes he or she is inevitably destined for Hell already. ´ Someone who believes he or she will never die. ´ Someone who believes there is someone else willing to make an irrational decision to purchase the bottle. Since the exchange rates of different currencies can fluctuate with respect to one another, it is also possible that the value of the bottle could increase from one transaction to the next even if the stated price decreases. This leads to an endless staircase-type paradox which would make it possible, in theory, for the bottle to keep getting sold infinitely many times. However, this might be forbidden depending on how the bottle imp interprets the idea of "selling at a loss".
Boy Or Girl Paradox
Release Date: //1959
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A two-child family has at least one boy. What is the probability that it has a girl? Authored by Martin Gardner.
Description: The Boy or Girl paradox surrounds a well-known set of questions in probability theory which are also known as The Two Child Problem,[1] Mr. Smith's Children[2] and the Mrs. Smith Problem. The initial formulation of the question dates back to at least 1959, when Martin Gardner published one of the earliest variants of the paradox in Scientific American. Titled The Two Children Problem, he phrased the paradox as follows: Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls? Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys? Gardner initially gave the answers 1/2 and 1/3, respectively; but later acknowledged that the second question was ambiguous.[1] Its answer could be 1/2, depending on how you found out that one child was a boy. The ambiguity, depending on the exact wording and possible assumptions, was confirmed by Bar-Hillel and Falk,[3] and Nickerson.[4] Other variants of this question, with varying degrees of ambiguity, have been recently popularized by Ask Marilyn in Parade Magazine,[5] John Tierney of The New York Times,[6] and Leonard Mlodinow in Drunkard's Walk.[7] One scientific study[2] showed that when identical information was conveyed, but with different partially ambiguous wordings that emphasized different points, that the percentage of MBA students who answered 1/2 changed from 85% to 39%. The paradox has frequently stimulated a great deal of controversy.[4] Many people argued strongly for both sides with a great deal of confidence, sometimes showing disdain for those who took the opposing view. The paradox stems from whether the problem setup is similar for the two questions.[2][7] The intuitive answer is 1/2.[2] This answer is intuitive if the question leads the reader to believe that there are two equally likely possibilities for the sex of the second child (i.e., boy and girl),[2][8] and that the probability of these outcomes is absolute, not conditional.[9]
Bracketing Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Is a "nuclear physicist" a physicist who had an accident, or is it just someone who studied nuclear physics?
Description: Is a "nuclear physicist" a physicist who had an accident, or is it just someone who studied nuclear physics?