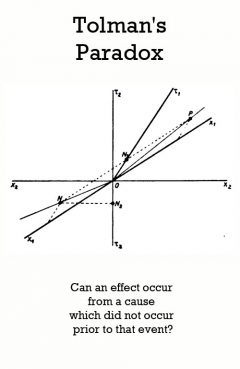
Tolman's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Can an effect occur from a cause which did not occur prior to that event?
Description: A tachyonic antitelephone is a hypothetical device in theoretical physics that could be used to send signals into one's own past. Albert Einstein in 1907 presented a thought experiment of how faster-than-light signals can lead to a paradox of causality, which was described by Einstein and Arnold Sommerfeld in 1910 as a means "to telegraph into the past". The same thought experiment was described by Richard Chace Tolman in 1917; thus, it is also known as Tolman's paradox. Causality paradox -- effects occur before the cause. In other words, the effect arises before the cause in this frame. Einstein (and similarly Tolman) concluded that this result contains in their view no logical contradiction; he said, however, it contradicts the totality of our experience so that the impossibility of a > c seems to be sufficiently proven.
Trinity Paradox
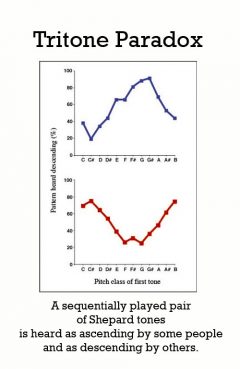
Tritone Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An auditory illusion in which a sequentially played pair of Shepard tones is heard as ascending by some people and as descending by others.
Description: An auditory illusion in which a sequentially played pair of Shepard tones is heard as ascending by some people and as descending by others.
Trouton-Noble Paradox or Right-Angle Lever Paradox
Tullock Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Rent-seekers seeking political favors can usually bribe politicians to give them the favors at a cost much lower than the value of the favor to the rent-seeker.
Description: The term Tullock paradox refers to the apparent paradox first observed by the public choice economist Gordon Tullock on the low costs of rent-seeking relative to the gains from rent-seeking. The paradox is basically that rent-seekers seeking political favors can usually bribe politicians to give them the favors at a cost much lower than the value of the favor to the rent-seeker. For instance, a rent seeker who hopes to gain a billion dollars from a particular political policy may need to bribe politicians only to the tune of ten million dollars, which is about 1% of the gain to the rent-seeker.
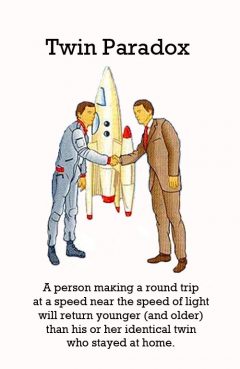
Twin Paradox (Twins? Paradox)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A person making a round trip at a speed near the speed of light will return younger than his or her identical twin who stayed at home.
Description: In physics, the twin paradox is a thought experiment in special relativity involving identical twins, one of whom makes a journey into space in a high-speed rocket and returns home to find that the twin who remained on Earth has aged more. The theory of relativity predicts that a person making a round trip will return younger than his or her identical twin who stayed at home. ///// When the traveling twin returns, he's younger and older than his brother who stayed put.
Two Envelopes Problem (aka The Exchange Paradox)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: You are given two indistinguishable envelopes and you are told one contains twice as much money as the other. You may open one envelope, examine its contents, and then, without opening the other, choose which envelope to take.
Description: The two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle, or paradox in logic, philosophy, probability, and recreational mathematics. It is of special interest in decision theory, and for the Bayesian interpretation of probability theory. Historically, it arose as a variant of the necktie paradox. The problem: You have two indistinguishable envelopes that each contain money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. You pick at random, but before you open the envelope, you are offered the chance to take the other envelope instead. It can be argued that it is to your advantage to swap envelopes by showing that your expected return on swapping exceeds the sum in your envelope. This leads to the absurdity that it is beneficial to continue to swap envelopes indefinitely. Example: Assume the amount in my selected envelope is $20. If I happened to have selected the larger of the two envelopes, that would mean that the amount in my envelope is twice the amount in the other envelope. So in this case the amount in the other envelope would be $10. However if I happened to have selected the smaller of the two envelopes, that would mean that the amount in the other envelope is twice the amount in my envelope. So in this second scenario the amount in the other envelope would be $40. The probability of either of these scenarios is one half, since there is a 50% chance that I initially happened to select the larger envelope and a 50% chance that I initially happened to select the smaller envelope. The expected value calculation for how much money is in the other envelope would be the amount in the first scenario times the probability of the first scenario plus the amount in the second scenario times the probability of the second scenario, which is $10 * 1/2 + $40 * 1/2. The result of this calculation is that the expected value of money in the other envelope is $25. Since this is greater than my selected envelope, it would appear to my advantage to always switch envelopes. A large number of solutions have been proposed. The usual scenario is that one writer proposes a solution that solves the problem as stated, but then another writer discovers that altering the problem slightly revives the paradox. In this way, a family of closely related formulations of the problem have been created, which are discussed in the literature. No proposed solution is widely accepted as correct.[1] Despite this it is common for authors to claim that the solution to the problem is easy, even elementary.[2] However, when investigating these elementary solutions they often differ from one author to the next. In the last two decades, several new papers have been published every year.[3]
Tzimtzum
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message:
Description: Tzimtzum: In Kabbalah, how to reconcile self-awareness of finite Creation with Infinite Divine source, as an emanated causal chain would seemingly nullify existence. Luria's initial withdrawal of God in Hasidic panentheism involves simultaneous illusionism of Creation (Upper Unity) and self-aware existence (Lower Unity), God encompassing logical opposites.
Ultraviolet catastrophe
Uncertainty Principle
Unexpected Egg Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An egg is concealed in one of ten boxes. You will not be able to deduce which box it is in before you open the box and see it.
Description: Imagine that you have before you ten boxes labeled from 1 to 10. While your back is turned, a friend conceals an egg in one of the boxes. You turn around. ñI want you to open these boxes one at a time,î your friend tells you, ñin serial order. Inside one of them I guarantee that you will find an unexpected egg. By ïunexpected' I mean that you will not be able to deduce which box it is in before you open the box and see it.î Assuming that your friend is absolutely trustworthy in all statements, can this prediction be fulfilled? Apparently not. Your friend obviously will not put the egg in box 10, because after you have found the first nine boxes empty you will be able to deduce with certainty that the egg is in the only remaining box. This would contradict your friend's statement. Box 10 is out. Now consider the situation that would arise if your friend were so foolish as to put the egg in box 9. You find the first eight boxes empty. Only 9 and 10 remain. The egg cannot be in box 10. Ergo it must be in 9. You open 9. Sure enough, there it is. Clearly it is an expected egg, and so your friend is again proved wrong. Box 9 is out. But now you have started on your inexorable slide into unreality. Box 8 can be ruled out by precisely the same logical argument, and similarly boxes 7, 6, 5, 4, 3, 2 and 1. Confident that all ten boxes are empty, you start to open them. What have we here in box 5? A totally unexpected egg! Your friend's prediction is fulfilled after all. Where did your reasoning go wrong?
The Unexpected Hanging Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The day of the hanging will be a surprise, so it cannot happen at all, so it will be a surprise. The surprise examination and Bottle Imp paradox use similar logic. Authored by Richard Montague.
Description: A judge tells a condemned prisoner that he will be hanged at noon on one weekday in the following week but that the execution will be a surprise to the prisoner. He will not know the day of the hanging until the executioner knocks on his cell door at noon that day. Having reflected on his sentence, the prisoner draws the conclusion that he will escape from the hanging. His reasoning is in several parts. He begins by concluding that the "surprise hanging" can't be on Friday, as if he hasn't been hanged by Thursday, there is only one day left - and so it won't be a surprise if he's hanged on Friday. Since the judge's sentence stipulated that the hanging would be a surprise to him, he concludes it cannot occur on Friday. He then reasons that the surprise hanging cannot be on Thursday either, because Friday has already been eliminated and if he hasn't been hanged by Wednesday night, the hanging must occur on Thursday, making a Thursday hanging not a surprise either. By similar reasoning he concludes that the hanging can also not occur on Wednesday, Tuesday or Monday. Joyfully he retires to his cell confident that the hanging will not occur at all. The next week, the executioner knocks on the prisoner's door at noon on Wednesday which, despite all the above, was an utter surprise to him. Everything the judge said came true.
Von Neumann Paradox
Release Date: //1929
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: One can break a planar figure such as the unit square into sets of points and subject each set to an area-preserving affine transformation such that the result is two planar figures of the same size as the original.
Description: In mathematics, the von Neumann paradox, named after John von Neumann, is the idea that one can break a planar figure such as the unit square into sets of points and subject each set to an area-preserving affine transformation such that the result is two planar figures of the same size as the original. This was proved in 1929 by John von Neumann, assuming the axiom of choice. It is based on the earlier Banach_Tarski paradox which is in turn based on the Hausdorff paradox. Banach and Tarski had proved that, using isometric transformations, the result of taking apart and reassembling a two-dimensional figure would necessarily have the same area as the original. This would make creating two unit squares out of one impossible. But von Neumann realized that the trick of such so-called paradoxical decompositions was the use of a group of transformations which include as a subgroup a free group with two generators. The group of area preserving transformations (whether the special linear group or the special affine group) contains such subgroups, and this opens the possibility of performing paradoxical decompositions using them.
Weyl's Paradox
Release Date: //1908
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message:
Description: The Grelling-Nelson paradox is a semantic self-referential paradox formulated in 1908 by Kurt Grelling and Leonard Nelson and sometimes mistakenly attributed to the German philosopher and mathematician Hermann Weyl.[1] It is thus occasionally called Weyl's paradox as well as Grelling's paradox. It is closely analogous to several other well-known paradoxes, in particular the Barber paradox and Russell's paradox.
Will Rogers Phenomenon
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Will Rogers (purportedly): When the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states.
Description: The Will Rogers phenomenon is obtained when moving an element from one set to another set raises the average values of both sets. It is based on the following quote, attributed (perhaps incorrectly)[1] to comedian Will Rogers: When the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states. The effect will occur when both of these conditions are met: -- The element being moved is below average for its current set. Removing it will, by definition, raise the average of the remaining elements. -- The element being moved is above the current average of the set it is entering. Adding it to the new set will, by definition, raise the average.
Willpower as a Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: People may do things better by focusing less directly on doing them.
Description: Those who kept their minds open were more goal-directed and more motivated than those who declared their objective to themselves. The idea that people may do things better by focusing less directly on doing them. That is: the direct exertion of willpower may not always be the most powerful way to accomplish a goal.
Winfree's Paradox
Yablo's Paradox
Release Date: //1993
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An ordered infinite sequence of sentences, each of which says that all following sentences are false. Authored by Stephen Yablo.
Description: Yablo's Paradox Yablo's paradox is a logical paradox similar to the liar paradox published by Stephen Yablo in 1993. Unlike the liar paradox, which uses a single sentence, this paradox uses an infinite sequence of statements, each of which refers to the truth values of the later statements in the sequence. Analysis of the statements shows there is no consistent way to assign truth values to all the statements, although no statement directly refers to itself. Implies there is no way to coherently assign a truth value to any of the sentences in the countably infinite sequence of sentences, each of the form, ñAll of the subsequent sentences are false.î